Nyligen kom jag i kontakt igen med räta linjens ekvation och linjära ekvationer och kom på att vi inte skrivit om det tidigare här på sidan, så detta inlägget tänkte jag dedikera till att täcka detta område i djupgående detalj, varje moment, varje tanke bakom och varje tillvägagångssätt man kan använda för att arbeta med denna typen av uppgifter.
Saker som kommer gås igenom kan ses i nedan lista:
- Definitionen av räta linjens ekvation (y=kx+m)
- Funktioner för räta linjens ekvation (f(x), g(x), etc.)
- k-värde
- m-värde
- Skärningspunkter / lösningar för 2 eller fler räta linjer
- y=0
- x=0
- x1 och x2
- Grafisk lösning av linjära ekvationer
- Grafisk hitta k-värde
- Användning av Grafräknare för att arbeta med räta linjens ekvation
- Tips för att rita räta linjer och grafer
- Matematisk formel för att räkna ut k-värde
- Insättning av x och y-värde för att lösa ut k och m-värde
- Koordinater och dess definition
- När en uppgift ”saknar lösning” och varför
- Hur man kan skriva i sitt anteckningsblock när man löser räta linjens ekvation och varför
- Horisontella och vertikala (lodräta) linjer
Vad är en rät linje?
Så om vi då börjar med vad en rät linje innebär, så kan vi visa det med hjälp av en simpel linjär ekvation med hjälp av det fina webbverktyget Wolfram Alpha som hjälper oss rita ut grafer (bland annat):
(Detta verktyget är super om ni inte skulle ha en grafräknare eller app som kan rita ut grafer i mobilen tillgänglig)

Räta linjer och Linjära ekvationer
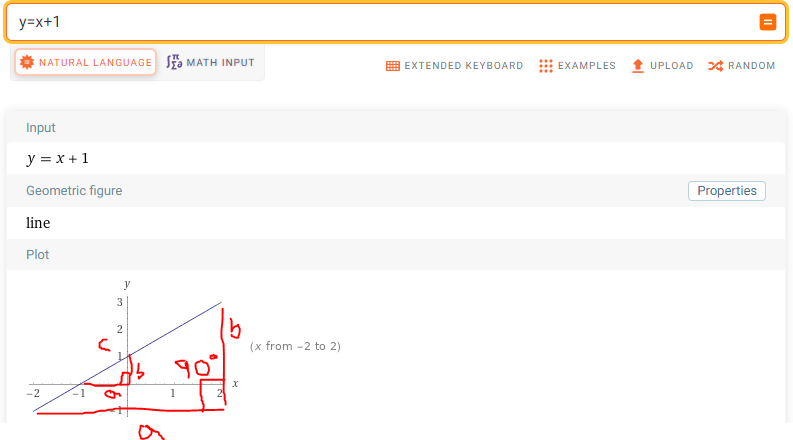
I ovan figur kan ni se att vår linjära ekvation vi valde för detta exemplet var:
\[ y=x+1 \]
Räta linjens egenskaper och beteende
Som ni kan se i figuren verkar linjen dras från negativa oändligheten i x-led till positiva oändligheten i x-led.
Räta linjens start och slutvärden
Med detta menar vi att vi inte har något ”slutvärde” på den negativa delen av x-axeln, och inte heller på den positiva delen av x-axeln – dock finns där fall där vi har det, men det är ett ämne för en annan artikel.
Räta linjens lutning
Linjen har också en lutning som vi senare kommer gå igenom mer i detalj, men som för stunden kan definieras som:
Antalet y-värden linjen ökar PER enstaka x-värde.
Och där finns många sätt både grafiska och rent matematiska att ta reda på detta värdet. Vi kommer gå igenom en hel del av dem (om inte samtliga).
Räta linjens skärningspunkter för X- och Y-axel
Vi kan också observera att vår linje skär både X-axeln i en specifik punkt/koordinat, såväl som Y-axeln.
Koordinatsystemets dimensioner/”fönsterstorlek” för utritande av rät linje
Och vi kan också notera graderingen Wolfram Alpha valt att rita ut för koordinatsystemet där vi ser ett ”fönster” som går från -2 x-led, till +2 i x-led och från -1 y-led till +3 y-led.
Pythagoras sats och trigonometri med räta linjer
Vi kan också notera (om ni är bekanta med trigonometri) att vår räta linje, kan liknas vid hypotenusan som vi kan räkna ut med hjälp av pythagoras sats. Därav ”Rät linje”. Där är 90 grader vinkel alltid mellan x-led och y-led om vi skulle dra ut streck för bas och höjd så det bildar en triangel.
Räta linjens ekvation
Formeln vi använder för att definiera alla räta linjer är som följer:
\[ y=kx+m \]
Vad denna innebär i detalj för att tydliggöra ytterligare är som följer:
\[ y=k*x+m \]
Från detta kan vi sen se att k-värdet hänger ihop med x-värdet. Vi kan även se att m-värdet är en ensamstående konstant.
Våra x och y-värden är variabler, detta innebär att de kan variera/bytas ut, medan både k-värdet och m-värdet är konstanter som är fasta för en rät linjes ekvation, de byts inte ut för en rät linje utan är alltid samma!
Med hjälp av formeln definierad ovan, kan vi för varje x-värde räkna ut ett y-värde om vi har k-värdet och m-värdet.
Lösa ut okända värden i räta linjens ekvation med hjälp av algebraisk ekvationslösning
Vi kan också använda algebraisk ekvationslösning för att lösa ut k, m, x och y så länge vi har 3 av 4 värden – t ex. har vi värde för x,y och k så kan vi lösa ut m-värdet, likaså kan vi lösa ut k-värdet om vi har x,y och m-värdet. Se nedan formel-omskrivning för hur detta kan användas:
(Sen finns där andra både matematiska och grafiska metoder för att lösa ut både k-värdet såväl som m-värdet som vi kommer gå igenom lite senare)
Med hjälp av matematisk omskrivning kan vi skriva om ovan definition av räta linjens ekvation som följer:
\[ y=kx+m =>y-kx-m=0 \]
Och därefter om 3 av 4 värden för k,x,m,y är kända så kan vi lösa ut den sista.
Räta linjer som ”funktioner” beroende av x
Det förekommer också att man pratar om ”funktioner” för räta linjens ekvation, en funktion hade kunnat beskrivas som:
En funktion är något som sker beroende av något annat.
I fallet om räta linjens ekvation brukar man definiera funktioner beroende av x är samma sak som y. Och det skrivs som:
\[ f(x)=y \]
Notera dock att det kvittar om vi skriver f,a,b,c,d,e,f,g eller något annat som ”funktion” av x. Bokstaven används bara som ett namn för själva funktionen, ungefär som x är namnet på vår okända variabel i algebraiska ekvationer. Har vi flera okända variabler i en ekvation kan de heta vad som helst, de hade kunnat heta a,b,c eller x,y,z.
Så, eftersom \( f(x)=y \) så kan vi också skriva följande definition av vår funktion f beroende av x:
\[ f(x) = kx+m \]
Så hur använder vi då funktioner i matematiken? Vi hade kunnat använda det för att definiera vad y-värdet av funktionen av x blir när x är satt till ett specifikt värde, med andra ord: värdet på y för ett specifikt x-värde. Det hade vi skrivit såhär:
\[ f(2)=k*2+m \]
Om x-värdet i funktionen är satt till 2 t ex. som i ovan exempel, så sätter vi bara in det x-värdet i vår ”funktion” (vilket är vår räta linjes ekvation i det här fallet: \( kx+m \)).
Så om vi låt säga utgår från vår linjära ekvation ovan: \( y=x+1 \) så kan vi skriva nedan för funktionen av x:
\[ f(x)=1*x+1 \]
\[ f(x)=x+1 \]
\[ f(2)=2+1 \]
\[ f(2)=3 \]
\[ y=3~när~x=3 \]
Oftast brukar \( f(x) \) vara ”standardfunktion” men det behöver som sagt inte vara det, och om där finns fler räta linjer och linjära ekvationer i en och samma uppgift, så brukar de döpas till \( f(x) \), \( g(x) \) osv. i bokstavsordning ökande fr. bokstaven f. Men återigen, det behöver inte vara så.
Räta linjens ekvations k- och m-värde förklarade
Låt oss nu gräva lite djupare i det här med k-värde och m-värde, vi börjar med k-värde.
k-värdet i räta linjens ekvation förklarat
Som vi skrev ovan så definierar vi k-värdet som:
Antal y-värden linjen ökar PER enstaka x-värde.
Man brukar också därmed kalla k-värdet för lutningen av linjen.
Om k-värdet är positivt så ”ökar” linjen med varje x-värde från vänster till höger, medan om k-värdet är negativt så ”dalar”/faller linjen från högre y-värde till lägre y-värde för varje x-värde från vänster till höger.
Hur vi tar reda på k-värdet för en rät linje i matematiken
Vi kan få fram vårt k-värde både grafiskt genom att observera en graf/utritad linje i ett koordinatsystem, eller genom att räkna fram det på olika sätt.
Hur vi grafiskt tar reda på k-värdet för en rät linje
Om vi börjar med hur vi får fram k-värdet/lutningen grafiskt så kan vi använda oss utav ovan utritade graf för vår räta linje vi hade i början \( y=x+1 \):

Nu är ju denna linje väldigt enkel, och vi kan se i bilden ovan att vår linje rör sig med att öka 1 y-värde PER x-värde.
För varje x-värde i högerled, ökar linjens y-värde med 1. Vilket ger oss ett k-värde på 1, \( k=1 \).
Hur vi matematiskt tar reda på k-värdet för en rät linje
Detta kan vi också se om vi granskar formeln: \( y=x+1 \) <- k-värdet kan inte vara 0 där, för då hade vi inte haft ett x (\( 0*x=0 \)).
k-värdet kan heller inte vara något annat än 1, då där står att vi bara har x, och det enda multiplicerat med x som blir x är talet 1!
Introduktion och förklaring av matematisk formel för att räkna ut k-värde (k-formel)
Där finns en matematisk formel man kan använda sig av för att räkna ut k-värdet för räta linjer som inte är lika enkla som ovan, formeln använder sig då av 2 olika punkter/koordinater på den räta linjen som vi vill ta reda på k-värdet för:
\[ (x_1, y_1)~och~(x_2, y_2) \]
Man kan tänka sig att k-värdet ges av (skillnaden i y) delat med (skillnaden i x) för 2 olika punkter/koordinater för den räta linjen vi vill räkna ut k-värdet för.
En koordinat brukar vi skriva som: \( (x,y) \), vilket vi kommer använda oss av för att tydliggöra hur denna matematiska formel för att räkna ut k-värdet fungerar.
För er som är intresserade av lite ”extra” så brukar skillnaden i matematik representeras av grekiska bokstaven Delta som ser ut som en triangel, alltså delta y delat med delta x ger k-värdet. Se nedan:
\[ \frac{\Delta y}{\Delta x} = \frac{(y_2-y_1)}{(x_2-x_1)}= k \]
Så om vi då utgår från vår ovan räta linje \( y=x+1 \) och väljer ut 2 punkter på linjen, låt säga: \( (1,2) \) och \( (3,4) \) så kan vi sätta in dessa värden i formeln för att räkna ut k-värdet ovan:
\[ (x_1,y_1)=(1,2)~och~(x_2,y_2)=(3,4) \]
\[ y_2=4,~y_1=2 \]
\[ x_2=3,~x_1=1 \]
\[ \frac{(4-2)}{(3-1)}=\frac{2}{2}=1=>k=1 \]
Prova själva genom att välja ut 2 andra valfria punkter på linjen i ovan bild 🙂
Viktigt att tänka på här är att alltid börja med x och y-värde från samma koordinat både i täljare och nämnare när man räknar ut skillnaden, så man inte råkar blanda ordningen!
T ex. börjar vi med koordinat/punkten \( (3,4) \) så måste vi börja med 4:an som y2 men även 3:an som x2.
Alternativt sätt att få ut k-värdet om vi har x-, y- och m-värde redan
Man kan som sagt också få ut k-värdet om vi har värdet för x och y (välj ut valfri punkt/koordinat på linjen för att få dessa värden) samt m-värdet (vart vår räta linje skär y-axeln (kan ses grafiskt, samt räknas ut för x=0)).
Ett exempel på detta är om vi säger att vi tar vår punkt som vi hade ovan: \( (1,2) \) och vet att m-värdet är 1 (kan grafiskt se i bild ovan att vår räta linje skär y-axeln i y=1), då kan vi skriva följande:
\[ y=kx+m => 2=k*1+1 \]
\[ 2=k+1=>2-1=k \]
\[ k=1 \]
Hur vi skriver när vi har fler än 1 svar på vår ekvation
Notera att x2 och x1 bara är två olika ”versioner” av x hade man kunnat säga, där vi skiljer dem åt genom att ge våra variabler av samma typ, olika definitioner så vi kan skilja dem åt när vi räknar.
Hur vi tar reda på m-värdet för en rät linje i matematiken
För att räkna ut m-värdet kan vi använda samma sätt om k-värdet är känt och vi har x- och y-värde för 1 punkt på vår räta linje.
Hur vi grafiskt tar reda på m-värdet för en rät linje
m-värdet som också grafiskt är skärningspunkten för vår räta linje i y-axeln (där linjen skär y-axeln) kan både ses grafiskt, såväl som räknas ut.
Hur vi matematiskt tar reda på m-värdet för en rät linje
Vi kan räkna ut vårt m-värde matematiskt genom att sätta in att \( x=0 \) i vår räta linjes ekvation/formel/funktion.
Där vår räta linje skär y-axeln är x alltid lika med 0 då ett koordinatsystems x- och y-axel sitter ihop vid Origo (punkt\( (0,0) \)).
En rät linjes skärningspunkter för X- och Y-axlarna förklarat
Likaså där vår räta linje skär x-axeln måste då y-värdet vara lika med 0.
Så när \( y=0 \) skär vår linje x-axeln och när \( x=0 \) skär linjen y-axeln.
Horisontella och lodräta linjer och hur de definieras och varför
På samma sätt som att \( y=0 \) ger oss en punkt där vår linje skär x-axeln, kan vi ha horisontella linjer som skrivs som \( y=2 \) t ex. För om vi tänker efter att \( y=kx+m \), och vår räta linjes ekvation är definierad som \( y=2 \), så innebär det att där bara finns ett m-värde, där finns inget k-värde, \( k=0 \), alltså ingen lutning, och då får vi en horisontell linje där y alltid är samma oavsett vilket x-värde.
En annan intressant sak är att vi på samma sätt får en lodrät linje om vi bara har \( x=2 \).
Hur vi hittar lösningen för 2+ räta linjer genom att hitta den gemensamma skärningspunkten (samma x- och y-värde för alla linjer)
När man pratar om ”grafisk lösning” av 2 eller fler linjer i en graf så brukar man syfta till att kolla upp skärningspunkt(er) för linjerna i grafen (där de korsar varandra). Se nedan bild:

Som ni kan se i ovan exempel har vi 2 st. räta linjer i vår graf som korsar varandra i en gemensam punkt. Detta är vad vi kallar för lösning.
Lösningen brukar skrivas som x= om 1 gemensam skärningspunkt, om flera kan man definiera de olika x-värdena som x1, x2, osv.
Som ni också kan se i ovan bild så om vi har ekvationerna \( y=kx+m \) för våra 2 räta linjer i grafen, då kan vi ställa de lika med varandra, för att lösa ut x:et för skärningspunkten!
Detta av anledning att båda ekvationerna står skrivna på formen \( y=kx+m \), där nyckeln är \( y= \) som är gemensam för båda två.
Om högerledet för ena linjen ger y-värde, kan man sätta ena ekvationens högerled (\( kx+m \)) lika med andra ekvationens högerled (\( kx+m \)) då även andra ekvationen ska ge y med sitt högerled 🙂 Detta brukar då kallas ”ekvationssystem”.
När räta linjers ekvationer och ekvationssystem inte skär varandra
Där kan ibland komma uppgifter som efterfrågar lösning för 2 linjer i en graf, där linjerna inte skär varandra någonstans, då säger man att uppgiften ”saknar lösning”!
Tillvägagångssätt förklarat för att ta reda på en rät linjes ekvation när du bara har graf/linje i koordinatsystem med graderade X- och Y-axlar
För att lösa räta linjens ekvation om du har en linje i en graf med okänd ekvation och bara har punkter du kan läsa ut på linjen, är första steget att räkna ut k-värdet med k-formeln:
\[ k=\frac{delta~y}{delta~x}= \frac{skillnaden~i~y}{skillnaden~i~ x}=\frac{(y_2-y_1)}{(x_2-x_1)} \]
När du sen väl fått ut k-värdet sätter du in värdet av valfri punkt på din linje i formeln \( y=kx+m \) där du redan satt in k-värdet du räknade ut, låt oss anta vårt k-värde var talet 3 t ex och vår utvalda punkt \( (1,2) \), då får vi:
\[ 2=3*1+m \]
Därefter kan vi använda oss utav vanlig algebraisk ekvationslösning för att lösa ut m-värdet.
När vi väl har både k-värde och m-värde kan vi sen skriva vår räta linjes ekvation, som i det här fallet blir:
\[ y=3x-1 \]
Tips för att rita ut en rät linje i ert anteckningsblock
Lite tips för när man ska rita ut en linje i en graf i sitt anteckningsblock kan vara att först pricka ut m-värdet på y-axeln (om ni har detta då förstås).
Därefter lite beroende på vilken information uppgiften har gett er, så kan ni försöka pricka ut ett minimum av 3 st. punkter på linjen (t ex. om ni fått m-värde och k-värde kan ni sätta x=1 och räkna ut y för när x=1 och på så vis få vart ni ska pricka in punkten på linjen där x=1).
När ni väl prickat ut 3 punkter på linjen i grafen kan ni sen lägga linjalen längs med och dra ett streck som blir er räta linje.
Rita upp räta linjer med hjälp av grafräknare eller annat tekniskt hjälpmedel
Om ni har tillgång till en grafräknare och vill använda den för att rita upp linjer kan ni trycka på knappen som heter ”y=” (utgår från en Texas Instruments TI-84) uppe i vänstra hörnet, därefter skriver ni in högerledet på er ekvation för linjen (\( kx+m \)) och sen trycker ni på ”Graph” högst upp till höger på räknaren. Så kommer räknaren rita ut er linje i graf.
Bonus: Justera fönsterinställningarna för er graf på grafräknaren (zooma in/ut i grafen)
Vill ni kan ni sen justera fönsterinställningar beroende på hur mycket ni vill ”zooma in” linjen och vilka värden som ska visas, ni kan då trycka ”Window” och sätta x-min, x-max, y-min, y-max där x-min är lägsta x-värde graf ska visa i fönstret (horisontalt), x-max likaså största x-värde att visa, y-min på samma sätt lägsta y-värde att visa (vertikalt) och y-max största att visa.